Hola a todos.
Esta entrada es mi primera contribución al blog, y siendo físico me gustaría comenzar con el que es el ladrillo de la física: el oscilador armónico.
El nombre, que nos da una idea de a qué nos estamos enfrentando, indica el movimiento de algo que se repite en el espacio y en el tiempo. Matemáticamente, siendo más estrictos, un movimiento armónico sería el descrito por una función “seno” o “coseno” . La palabra “armónico”, procedente del griego, nos da la idea de una conveniente proporcion y correspondencia entre unas y otras cosas. El concepto aparece en música, como la unión de sonidos acordes, y Kepler (amante de la música y con su mente puesta en ella) lo utilizaba como expresión de belleza y unión entre las matemáticas y el movimiento celeste. [Vease “La armonía de los mundos“]
Recuerdo que alguien me dijo en mi primer año de carrera que “la física, al final, se reduce al oscilador armónico”. No voy a admitir la certeza de esta frase, pues sería reduccionista, pero si es verdad que este concepto de oscilador armónico (a partir de aquí OA) plaga la física moderna en casi todos sus campos: física de particulas, óptica, termodinámica, … son solamente algunos de los lugares dónde se utiliza, en algún momento, esta idea.
Pero hoy no voy a hablar de todas estas ramificaciones de la teoría. Ya habrá tiempo. Hoy describiré un fenómeno aparentemente simple en el que, bajo ciertas aproximaciones, podemos observar este tipo de movimiento: un péndulo bajo la acción de la gravedad cerca de su estado de reposo.
Esta tarea la llevaremos a cabo utilizando el formalismo Newtoniano que es el primero aprendido por (casi) cualquier estudiante de física y el más instructivo en tanto es el menos abstracto de los posibles.
Para empezar, escribamos la ecuación fundamental que nos permitirá describir el movimiento del péndulo: la segunda ley de Newton. Es una ecuación diferencial de segundo orden [1] que nos describe la evolución dinámica del sistema. Tiene la forma
,
donde podemos leer que la suma de fuerzas actuando sobre un cuerpo de masa constante
provoca una aceleración
en este y que, a igualdad de fuerzas, un cuerpo con una masa mayor experimentará una aceleración menor.
Este último punto es algo que experimentamos todos los días: si suponemos que nosotros aplicamos la misma fuerza a dos objetos, nos cuesta más mover uno que tiene más masa que uno más liviano. ¡Ruego cautela, pues la distinción entre masa y peso es sutil pero importante!: masa es la cantidad de materia que hay en un cuerpo y peso es la acción de la gravedad sobre ese cuerpo; y aunque, en general, utilicemos la palabra “peso” para medir la masa (con unidad el kilogramo, kg) de las cosas, las unidades correctas de peso en el Sistema Internacional serían “Newtons” (N, la unidad de fuerza)
Otro detalle importante es el caracter vectorial de esta igualdad. Si aplicamos una fuerza en una dirección sobre un cuerpo, éste se verá acelerado en la misma dirección y sentido en que aplicamos la fuerza. Nosotros, al contrario, sentiremos una fuerza de la misma dirección y sentido opuesto a ésta -la denominada tercera ley de Newton.
Esto es, no obstante, una aproximación, pues hay muchas veces en que al aplicar una fuerza sobre un cuerpo éste se ve deformado o transforma nuestro movimiento en calor impidiendo que la fuerza se convierta de manera efectiva en aceleración. Ésta aproximación que utilizaremos nosotros se llama del “punto material”, pues supondremos que el cuerpo sobre el que actuamos se reduce a un punto, donde está su masa, y que éste responde de acuerdo con la segunda ley de Newton a nuestra fuerza.
Una vez hemos aclarado las primeras condiciones bajo las que describiremos nuestro movimiento, vamos a esquematizar el sistema al que nos estamos enfrentando:
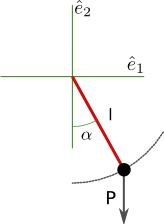
Diagrama de un péndulo bajo la acción de la gravedad, mostrando el sistema de coordenadas y el vector peso.
Este gráfico representa un péndulo de masa que oscila en un entorno del origen de coordenadas a una longitud
desde un punto fijo. Supondremos además que la sujeción de la masa al punto fijo no contribuye a la masa total.
y
representan, respectivamente, los vectores unitarios en la dirección horizontal y vertical del sistema cartesiano de coordenadas fijo con respecto al observador,
. Si el péndulo se desplaza un ángulo
desde la vertical, su posición vendrá descrita por el vector
. El peso
del cuerpo, o la fuerza gravitatoria que actua sobre el punto
donde está centrada la masa del objeto tiene un valor
Esta fuerza actúa en dirección vertical, y el signo negativo nos indica que siempre apunta hacia abajo (con respecto a nuestro sistema de referencia). Cuanta más masa tenga el cuerpo, mayor será la fuerza que experimente, pero esto no implica que la aceleración que experimente se vea aumentada; de hecho, es falso, como ya averiguase Galileo Galilei y escribiese en su libro “Discurso y demostración matemática, en torno a dos nuevas ciencias”
De hecho, si solamente actuase la fuerza de la gravedad, al sustituir por
en la segunda ley de Newton podríamos observar que la aceleración es independiente de la masa de la particula y siempre sería en dirección vertical y sentido negativo. En el caso de un péndulo esto es contrario a la intuición, pues la masa que compone el péndulo no “cae” hacia abajo, sino que gira entorno a un punto fijo a una cierta longitud
. Esto nos permite inferir la presencia de otra fuerza, la tensión
, que mantiene al cuerpo en su trayectoria circular. Podríamos escribir las ecuaciones del movimiento como:
.
Esto nos daría dos ecuaciones, una para cada componente cartesiana, que describirían el movimiento de la masa. Sin embargo, necesitaríamos saber el valor de para poder resolverlas. Pero ¿cómo es esta fuerza? A priori no tenemos ningún conocimiento sobre su magnitud. Lo único que sabemos es que la tensión es tal que impide al cuerpo salirse de la trayectoria.
Para describir la tensión necesitamos saber cómo se v modificada la trayectoria de nuestro objeto bajo la acción de dicha fuerza. De modo que observaremos lo que ocurre en un entorno del punto en el que está el objeto. Esto es, miraremos al sistema desde el sistema de referencia centrado en el objeto,
. Definiremos la dirección vertical
apuntando siempre hacia el centro del movimiento, asi que “arriba” será nuestro punto fijo. De este modo, trasladando el centro de coordenadas hacia el punto donde se concentra la masa, la trayectoria vista desde este sistema de referencia será en la dirección de
, “hacia adelante y hacia atrás”. Si tenemos este sistema bien definido, deberíamos ser capaces de describir este marco de referencia como una transformación del original,
:
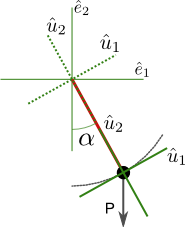
Nuevo sistema de coordenadas
Esta transformación no es nada más y nada menos que la de un giro de ángulo $\alpha$. Podemos ver que cuando la transformación se reduce a la identidad, de modo que recobramos el sistema de referencia original. Podemos trasladar de este modo cualquier vector desde el sistema de referencia original,
hasta el centrado en el objeto,
. Asi, cualquier vector podrá ser expresado como sus proyecciones en las direcciones
y
.
¿Por qué hacer un cambio de coordenadas si, al final, vamos a tener que trabajar con vectores? Desde es posible ver de manera más clara cómo tiene que ser la tensión. Si en este sistema de referencia el movimiento tiene que ser en la dirección
, la suma de fuerzas expresada en estas coordenadas,
ha de tener componente vertical nula. De cualquier otro modo, el objeto se movería en la dirección que une al cuerpo con el punto fijo, ¡pero hemos fijado esa distancia!.
Este hecho podemos escribirlo matemáticamente como:
Además, y dado que la tensión solamente actua en la dirección que une al cuerpo con el punto fijo de giro, la componente horizontal de la tensión en será nula, esto es
El peso es conocido en el sistema original , de modo que podemos transformarlo en el original utilizando el cambio de coordenadas anteriormente descrito:
de modo que la tensión es
.
¡Ya tenemos la tensión! Hemos explotado la restricción del movimiento para obtener información sobre dicha fuerza.
Ahora, para completar el planteamiento del problema original, solamente tenemos que trasladar la tensión de vuelta al sistema original utilizando la transformación inversa a la dada:
En , como esperaríamos, la componente horizontal de la tensión es 0 y la vertical iguala al peso en magnitud de modo que ambas fuerzas se equilibran. Utilizando la igualdad
, podemos obtener
Asi que ya podemos escribir la segunda ley de Newton para cada una de las componentes:
,
donde e
representan la aceleración de las componentes horizontal y vertical respectivamente. Estas ecuaciones, dentro de las aproximaciones hechas, son “exactas” y representarían la evolución del sistema tal y como lo hemos descrito.
Sin embargo, las ecuaciones así descritas son no-lineales, pues el miembro de la izquierda de ambas expresiones depende de manera no lineal de x e y (recordemos que depende de x e y, pues nos lleva de uno a otro sistema de coordenadas) y la solución es una expresión complicada utilizando las funciones elípticas de Jacobi de tipo seno .
¿Hemos de contentarnos con esto? Ya hemos hecho muchas aproximaciones, de modo que ¿por qué no una mas?
En muchas situaciones podemos suponer que las oscilaciones que realiza el péndulo en torno a su punto de equilibro estable (el origen de coordenadas) tienen una amplitud muy pequeña. Esto se cumplirá si el péndulo tiene una longitud muy grande, o si se le aplica un desplazamiento inicial pequeño o suave. Esto es equivalente a exigir que la energía del sistema sea muy pequeña.
Bajo estas condiciones, son válidas las siguientes aproximaciones
,
,
donde hemos realizado una serie de Taylor cerca del punto sabiendo que
Si sustituimos en las ecuaciones de movimiento:
.
¡Esto tiene mucha mejor pinta!: la segunda ecuación nos dice que la altura (representada por la coordenada ) no variará, lo cual es válido dentro de nuestra aproximación de pequeña amplitud de oscilación, mientras que la primera es una ecuación lineal de segundo orden “sencilla”. Además, nos dice que la evolución del sistema no depende de la masa del objeto, cosa en principio “poco intuitiva” pero que puede ser demostrado mediante un experimento sencillo.
Estamos, damas y caballeros, cerca del final, pues la conclusión de un problema dinámico reside en la descripción de las trayectorias que regirán el movimiento. La solución más general de esta ecuación del movimiento es una suma de un seno y un coseno, que puede ser reexpresada mediante un solo coseno,
siendo y
determinadas por las condiciones iniciales del sistema. Así, por ejemplo, si el cuerpo parte en
desde el punto
sin velocidad inicial, los coeficientes que determinan su evolución serán
y
.
¿Podéis ver ya el por qué del nombre de esta entrada? Hemos conseguido, tras una serie de aproximaciones, reducir el problema del movimiento de un péndulo bajo un campo gravitatorio a una expresión con un coseno. Esto es, a un “oscilador armónico”.
Me gustaría hacer notar que una de las aproximaciones que hemos utilizado para llegar a este resultado es que el sistema debía moverse con poca energía alrededor de un punto de equilibrio. Esta es la aproximación que permite simplificar las ecuaciones del movimiento y convertir un problema intratable en uno cuya solución es (bajo las aproximaciones mencionadas) una función seno o coseno. Quizás hemos perdido en generalidad, pues nuestra solución no se puede aplicar a todos los casos, pero hemos ganado en comprensión, al poder tener una expresión sencilla que describa el movimiento.
Aunque aún es pronto para aprehenderlo completamente, este buen comportamiento en algunos sistemas tiene consecuencias que van más allá de las ecuaciones de Newton y la física clásica. Hay algo inherente en ciertos sistemas que permite que su descripción se vea simplificada, aunque estas propiedades no sean evidentes bajo la luz de las leyes de Newton.
En las próximas ediciónes nos adentraremos en el apasionante mundo de la mecánica analítica para ver si somos capaces, bajo los ojos de Lagrange y Hamilton, de comprender mejor esta clase de sistemas.
[1] George F. Simmons, “Ecuaciones Diferenciales con Aplicaciones y Notas Históricas” Segunda Edición, McGraw-Hill España (1990)

Pingback: Introducción al cálculo variacional en la física | Scientia potentia est
Pingback: ¿Qué es exactamente una EDO? | Scientia potentia est
Pingback: Oscilador Armónico – Parte II | Scientia potentia est