Siempre me ha resultado curioso la facultad sorpresiva de la Naturaleza. Nos empeñamos en admirar lo compleja que es en cada detalle. Y después descubrimos que, si miramos desde el punto de vista adecuado, todo es simple. Los científicos nos inventamos leyes (de acuerdo con unas observaciones) para intentar comprender cómo funciona, y al final basta con unos pocos principios fundamentales para derivar el resto.
Al principio estas leyes suelen ser engorrosas, pues de manera experimental intentamos contrastar nuestras observaciones con funciones que se asemejen a nuestros resultados con el fin de poder predecir más fenomenología. Así le ocurrió a Kepler que, habiendo heredado los datos de Tycho Brahe y teniendo observaciones de altísima calidad, enunció las tres leyes que llevan su nombre. Estas leyes requirieron de mucho trabajo experimental y análisis de datos para ser obtenidas y son todo un triunfo de la ciencia. Sin embargo, como en todos los campos científicos, son solo una aproximación de la realidad e introducir perturbaciones (dadas por otros planetas) eran necesarias para poder reproducir con más detalle los resultados.
Más tarde, arduos razonamientos acerca de las observaciones suelen llevar a refinamientos de la teoría. De este modo, Newton propuso la “ley de la gravitación universal” que, aplicada a un sistema simple bajo ciertas suposiciones, ¡daba como resultado las leyes de Kepler!
En el ejemplo anterior, afortunado donde los haya, no he querido entrar en las teorías anteriores de epiciclos y deferentes. Estas “teorías” se ajustaban muy bien a los datos experimentales y por eso tardaron tanto en ser desbancadas. Sin embargo, recientemente se ha demostrado que dado un número suficiente de epiciclos y deferentes, se puede reproducir cualquier órbita, pero esto no nos interesa… lo que queremos es saber cómo son las cosas y, en general, predecir el comportamiento de los sistemas de acuerdo con nuestro conocimiento: si nuestro método puede dar como pronóstico cualquier cosa , la realidad deja de tener sentido y pasa a ser un caso particular, en vez de ser el sujeto central de lo que nos atañe.
Por eso es tan importante la simplicidad. El objetivo de todo científico es poder hacer prediciones sobre el comportamiento de la realidad; si está descrito de manera muy compleja es posible que no estemos teniendo en cuenta los parámetros y simplificaciones adecuados para nuestro sistema en cuestión.
Supongo que algo así deberían tener en la mente los científicos y matemáticos de los siglos XVIII y XIX cuando fundaron lo que se denominó “mecánica analítica”. Para ello, utilizaron el metafísico “principio de mínima acción” que plantea, en palabras de Maupertuis [1] que
“…la Naturaleza siempre actúa de la manera más simple posible para producir sus efectos.”
Y… ¿para qué sirve este principio? Voy a ilustrarlo con un ejemplo de mecánica clásica. Queremos saber qué camino tomará un cuerpo en una cierta situación. Imaginemos que tenemos una cantidad (un funcional, matemáticamente hablando), a la que llamaremos acción, que depende del “camino” que ese cuerpo toma en su movimiento. Esa acción puede ser calculada para cada cualquier camino siempre y cuando tenga una cierta regularidad. Pues bien, el camino real, el que tomará el cuerpo y que podrá ser predicho, es aquel que hace de la acción un mínimo (más rigurosamente, un valor estacionario). Esto es “fácil” de entender:
Si calculamos la acción para todos los caminos, escogemos el camino que tiene la acción más pequeña, esa trayectoria es nuestra solución.
Simple, ¿no?
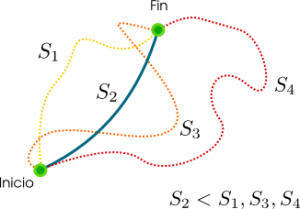
Si a cada posible trayectoria de un cuerpo entre los puntos inicial y final de su trayectoria se le asigna una acción S, la trayectoria real será aquella que tenga la acción menor. Aquí, la segunda trayectoria 2 será la real, por tener la acción menor al resto.
Pensémoslo por un segundo… ¿no es cierto que el número de caminos posibles es infinito? ¡¿Tenemos que calcular la acción para todos los posibles caminos?!
La respuesta es “no”. Hete aquí la belleza de la Naturaleza y del ingenio humano. Matemáticamente es un poco engorroso de explicar, y se necesita alguna fórmula, de modo que dejaré tan engorrosa tarea a Rafa, más versado que yo en estos temas.
Uno de los trabajos de la física es averigüar cuál es la definición correcta de acción que nos da resultados que se correspondan con el comportamiento de la Naturaleza.
Por mi parte, y como estaba planeado, escribiré sobre las dos principales ramas de esta teoría en la física, el método Lagrangiano y Hamiltoniano, utilizando como guía el oscilador armónico. De este modo, comprenderemos un poco mejor las ventajas y desventajas de este método en comparación con la mecánica vectorial de Newton (de la que ya hablamos aquí)
Por último, una reflexión:
Simplicidad no implica que vaya a ser fácil obtener un resultado correcto. Simplicidad implica que puedes contárselo a tu abuela (de una manera más o menos burda).
En estas lineas, Euler dejó escrito [2]:
“Comparados con los métodos de la mecánica tradicional, puede ser que el movimiento sea más dificil de calcular utilizando nuestro nuevo método; sin embargo, parece más fácil de comprender desde primeros principios.”
Referencias:
[1] Maupertuis, Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles (1744) (Traducción inglesa, original en francés) Nótese que aplica su sistema a la óptica, como lo hizo antes Fermat.
[2] Euler, Metodus inveniendi. Additamentum II (1744) (traducción inglesa)
[3] Cornelius Lanczos. The variational principles of mechanics (1949)
(Esta entrada es una contribución al XV Carnaval de la Física alojado por Curiosidades de la Microbiología)

Pingback: Introducción al cálculo variacional en las matemáticas | Scientia potentia est
Pingback: El enigma de Hooke | Scientia potentia est